A maioria dos grandes matemáticos descobriu esse tópico quando eram jovens e muitas vezes se destacam em competições internacionais.
Por outro lado, a matemática era um ponto fraco para June Huh, nascida na Califórnia e criada na Coreia do Sul. “Eu era bom na maioria das matérias, exceto em matemática”, disse ele. “A matemática foi notavelmente medíocre, em média, o que significa que em alguns testes tive um desempenho razoavelmente bom, mas em outros quase falhei.”
Quando adolescente, o Dr. Huh queria ser poeta e passou dois anos após o colegial perseguindo essa busca criativa. Mas nenhum de seus escritos foi publicado. Quando frequentou a Universidade Nacional de Seul, estudou física e astronomia e considerou uma carreira como jornalista científico.
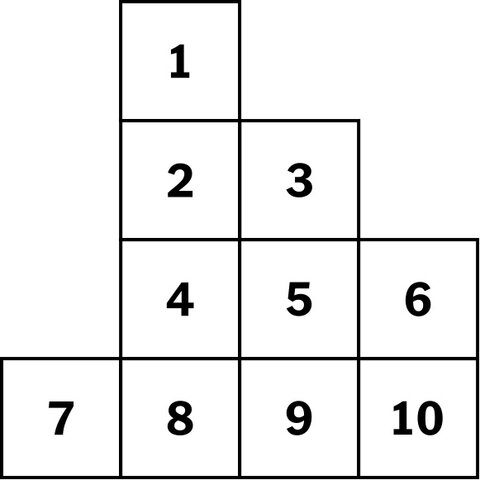
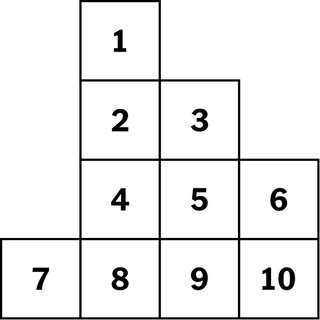
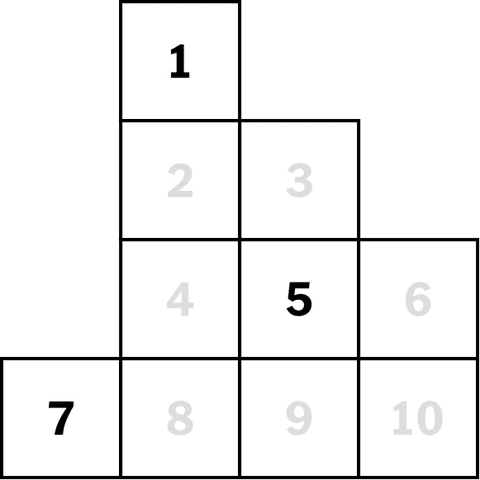
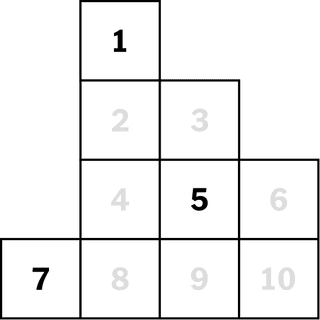
Olhando para trás, ele reconhece flashes de percepção matemática. No ensino médio nos anos 90, ele estava jogando um jogo de computador, “The 11th Hour”. O jogo apresentava um quebra-cabeça de quatro cavaleiros, dois deles pretos e dois brancos, colocados em um tabuleiro de xadrez estranhamente pequeno.
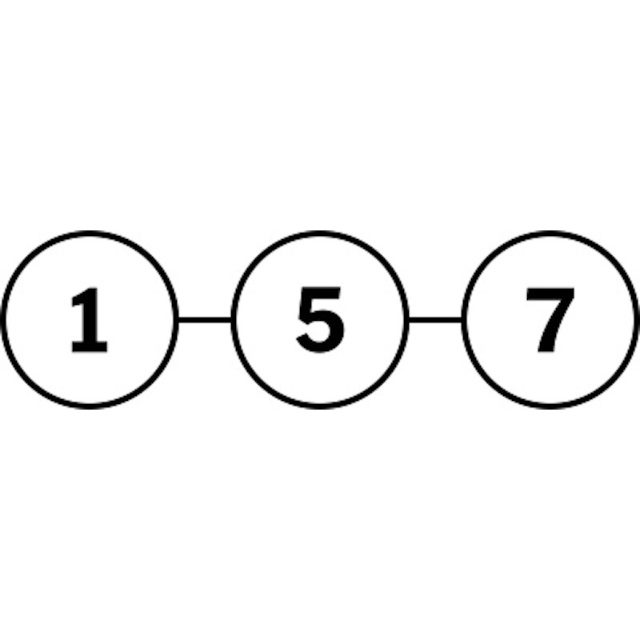
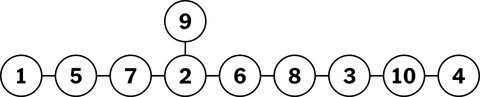
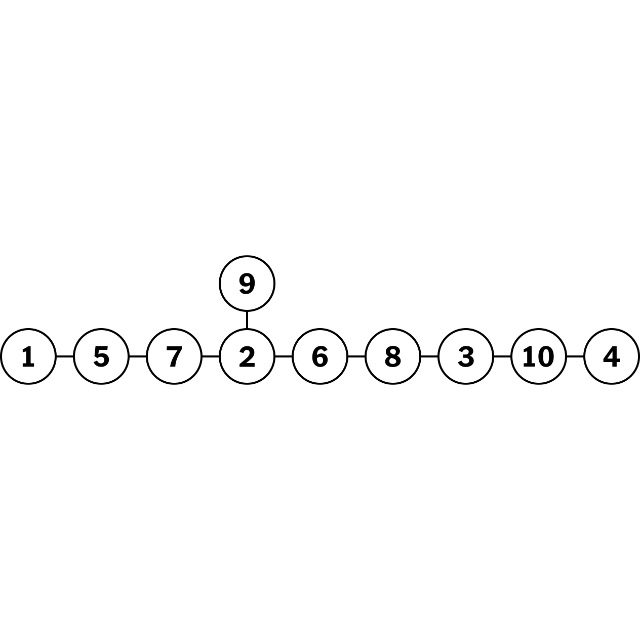
A tarefa era trocar as posições dos cavaleiros preto e branco. Ele passou mais de uma semana caindo antes de perceber que a chave era encontrar as casas para as quais os cavalos poderiam se mover. O quebra-cabeça de xadrez pode ser reformulado como um gráfico onde cada cavalo pode se mover para um espaço adjacente desocupado, e a solução pode ser vista com mais facilidade.
Reformular os problemas matemáticos simplificando-os e traduzindo-os de uma forma que torne a solução mais clara tem sido a chave para muitos dos avanços. “As duas fórmulas são logicamente indistinguíveis, mas nossa intuição funciona em apenas uma delas”, disse o Dr. Huh.
quebra-cabeça de raciocínio matemático
quebra-cabeça de raciocínio matemático
por aqui Quebra-cabeça venceu Jun huh:

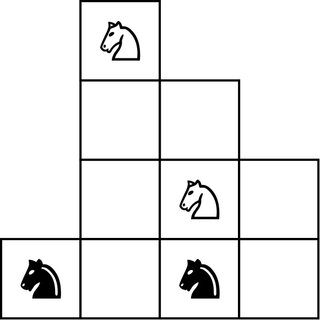
Meta: Os cavaleiros preto e branco trocam de posição. →
Ele só descobriu a matemática novamente no último ano da faculdade, aos 23 anos. Naquele ano, Hisuki Hironaka, o matemático japonês que ganhou a Medalha Fields em 1970, era professor visitante na Universidade Nacional de Seul.
Dr. Hironaka estava dando uma aula de geometria algébrica, e Dr. Huh participou, muito antes de receber seu Ph.D., pensando que poderia escrever um ensaio sobre o Dr. Hironaka. “Ele é como uma estrela na maior parte do leste da Ásia”, disse o Dr. Huh sobre o Dr. Hironaka.
Dr. Huh disse que o curso inicialmente atraiu mais de 100 alunos. Mas logo a maioria dos alunos achou o material incompreensível e desistiu da aula. Dr. Huo continuou.
“Depois de três palestras, havia cinco de nós”, disse ele.
O Dr. Huo começou a almoçar com o Dr. Hironaka para discutir matemática.
“Ele estava falando comigo principalmente”, disse o Dr. Huh, “e meu objetivo era fingir que entendia algo e responder da maneira certa para que a conversa continuasse. Foi uma tarefa difícil porque eu realmente não sabia o que estava acontecendo.”
Dr. Huh se formou e começou a trabalhar em seu mestrado com o Dr. Hironaka. Em 2009, quando o Dr. Huh se candidatou a cerca de uma dúzia de escolas de ponta nos Estados Unidos para seu doutorado.
“Eu estava bastante confiante de que, apesar de todos os cursos de matemática reprovados em minha transcrição de graduação, eu havia recebido uma carta entusiasmada de um medalhista Fields, então eu seria aceito em muitas escolas de pós-graduação.”
Todos, exceto um, o rejeitaram – a Universidade de Illinois Urbana-Champaign o colocou em uma lista de espera antes de finalmente aceitá-lo.
“Foram algumas semanas muito interessantes”, disse o Dr. Huh.
Em Illinois, ele começou um trabalho que o trouxe à tona no campo das combinações, o campo da matemática que quantifica o número de maneiras pelas quais as coisas podem ser misturadas. À primeira vista, parece brincar com a Tinker Toys.
Pense em um triângulo, um objeto geométrico simples – o que os matemáticos chamam de grafo – com três arestas e três vértices onde as arestas se encontram.
Pode-se então começar a fazer perguntas como, dado um determinado número de cores, quantas maneiras existem para colorir os vértices, já que nenhum deles pode ser da mesma cor? A expressão matemática que dá a resposta é chamada de polinômio cromático.
Polinômios cromáticos mais complexos podem ser escritos para objetos geométricos mais complexos.
Usando ferramentas de seu trabalho com o Dr. Hironaka, Dr. Ho provou a conjectura de Reed, que descrevia as propriedades matemáticas desses modificadores de contorno cromáticos.
Em 2015, Dr. Huh, juntamente com Eric Katz da Universidade Estadual de Ohio e Karim Adepracito da Universidade Hebraica de Jerusalém, demonstraram a teoria de Rota, que envolvia objetos combinatórios mais abstratos conhecidos como matróides em vez de triângulos e outros gráficos.
Para os matróides, existe outro grupo de polinômios, que apresentam comportamento semelhante aos polinômios cromáticos.
Sua prova foi puxada para uma peça mística de geometria algébrica conhecida como teorema de Hodge, em homenagem a William Vallance Douglas Hodge, um matemático britânico.
Mas o que Hodge desenvolveu, “foi apenas um exemplo dessa manifestação misteriosa e universal do mesmo padrão em todas as disciplinas matemáticas”, disse o Dr. Huh. “A verdade é que nós, mesmo os maiores especialistas neste campo, não sabemos realmente o que é.”

“Praticante do Twitter. Analista. Desbravador de TV sem remorso. Especialista em bacon. Fanático pela Internet.”